高炉炼铁过程的数学模拟

来源：储满生1 胡涛2 李子林2 沈峰满1 |浏览：次|评论：0条 [收藏] [评论]

高炉炼铁过程的数学模拟

储满生¹ 胡涛² 李子林² 沈峰满¹

(1．东北大学钢铁冶金研究所，辽宁沈阳 110004；2．安阳钢铁集团公司技术中心，河南安阳455004)

摘要本文简述全高炉反应动力学数学模型的发展历程后，详细介绍了该类模型的最新研究成果一基于多流体理论而创建的多流体高炉数学模型，并利用实际测量值对该模型的有效性进行了验证。该模型是一个较为复杂而全面的高炉过程模拟工具，可有效分析处理多维问题。最后，对高炉数学模型的未来发展做出了若干展望。

关键词高炉；数学模型；多流体理论；炼铁；计算流体力学

在高炉操作过程中，由炉顶加入炉料，从炉缸渣铁口排放渣铁；而从风口鼓人热风和喷吹煤粉'产生煤气从炉顶逸出。所以可将高炉看作是存在炉料下降和煤气上升两个逆向运动的反应器，高炉内所有传输现象和反应都发生于炉料与煤气的向流运动中。

高炉内多种多相物质共存且相互作用，而且诸多物理化学现象同时发生，故高炉在化工领域被认为是最复杂的冶金反应器之一。随着现代测控技术的发展和对实际运行高炉的炉体解剖，人们获得了大量有用数据，对高炉有了更深的理解，但仅凭这些仍很难详细掌握炉内的现象。因此，为了更好地理解、控制和改进高炉炼铁过程，更多的努力用于开发高炉数学模型^［¹^］。根据对高炉内传输现象描述方法的不同，数学模型分为平衡理论模型、热化学模型和反应动力学模型；按所考虑的空间坐标维数，分为一维、二维和三维模型；按考虑时间变量与否，有稳态模型和非稳态模型^［¹^—2^］。

高炉炼铁技术在过去几十年里获得了巨大的进步。为了提高产量、降低能耗和减少环境负荷，大量新技术，如喷吹煤粉和有效利用含碳含铁废弃物不断被采用，高炉的功能不断扩大。随之而来，炉内现象更趋复杂化。而建立在反应动力学和传输现象理论基础上的反应动力学数学模型是一个有用的工具，可用于详细分析炉内状态和精确预测高炉操作性能。

1 高炉数学模型的发展

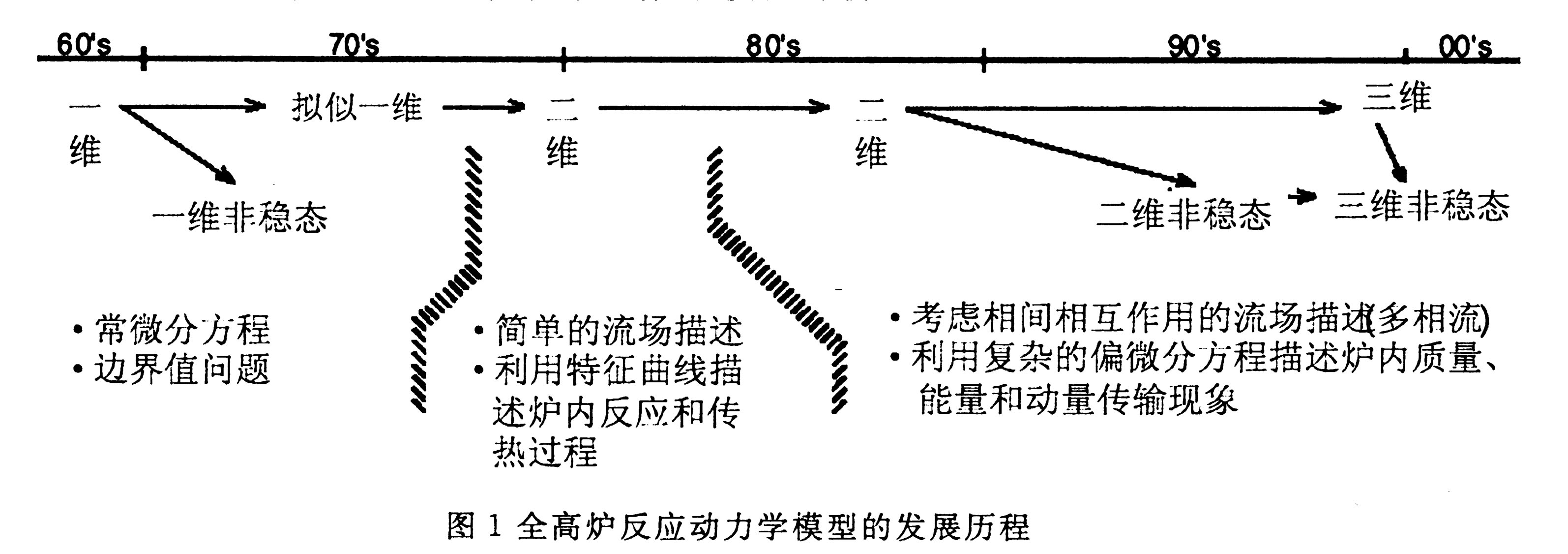
最早获得发展的是高炉一维模型，且先有稳态模型，随后逐渐发展为非稳态。鞭严等人在20世纪60年代末开发的高炉稳态一维模型最具代表性^［²^］。在鞭的模型中，考虑了炉内主要化学反应和传热过程，模拟结果给出了主要工艺变量沿高炉高度方向上的分布。后来，许多研究者仿效鞭严的建模思想建立了一系列用于解决不同问题的高炉数学模型。这些早期的高炉模型很好地把握了对局部和全高炉的能量平衡和物质平衡这一基本规律，因而在模拟高炉现象、分析操作参数对炉况和冶炼指标的影响、指导开停炉等方面获得了相当的成功，如一些模型应用于分析鼓风压力波动对高炉操作的影响、预测最低燃料比以及模拟高顶压操作等实践^[2]。但是对于一维的高炉模型来说，过程参数被假设为径向均匀分布，而高炉的解剖和取样分析证实气体温度和炉内物质成分等在径向上都是不均匀的。另外，在这些模型的建模过程中，炉内物质和能量的传输过程只能通过常微分方程来描述。再加上边界值设定不合理等缺陷，这些早期一维模型的预测精度和应用范围都很有限。

到了80年代，计算机技术的发展允许模型处理更大的矩阵，新建立的模型可以采用偏微分方程作为它们的控制方程。在这期间，大量二维高炉模型被开发，其中较为知名的有Hatano和Kurita的模型，Yagi、Takeda和Omori的模型，Sugiyama和Sugata的BRIGHT模型^[1^，2]。二维模型主要被用于描述炉内更为复杂的现象，评估操作条件对高炉操作性能和炉况的影响，分析软熔带的变化和影响，模拟和开发高炉炼铁新技术等方面。总体来说，这些模型对指导实际高炉操作和促进炼铁技术的进步做出了一定的贡献。

到90年代初，一个基本概念“多流体理论”被提出，即用多相流和相间双向相互作用来描述发生在炉下部的现象，而且炉内物质相应通过流动机制来加以区分。因此，除了最基本的物质三态(气、固、液)外，被炉内气流挟带的未燃煤粉被处理为一个独立的粉相^［³^］。在随后基于这个理论而发展的高炉数学模型中，根据物性的不同，液相又被划分为渣相和铁水相，而粉相分为静态滞留粉相和动态滞留粉相。这些模型都总称为“多流体高炉数学模型^［4^—7^］”，是较为复杂全面的高炉动力学模型。目前，多流体模型能够较合理地处理二维和三维问题，并应用于超高效率高炉炼铁技术的数学模拟评价^［⁸^—10^］。

2 多流体高炉数学模型

2．1 模型框架

多流体高炉数学模型基于多流体理论、冶金传输原理、反应动力学以及计算流体力学等理论模拟高炉炼铁过程[4，5，7]。模型主要考虑了从渣面到料面的整个填充区域，而且认为高炉是轴对称的。多流体模型中，将气相、固相(焦炭和含铁炉料)、铁水、熔渣和喷吹粉体分别视为具有各自流动机制的相，每相由一个或多个组元组成，且每个组元具有独立的成分和物性。模型中考虑的物质和相如表1所示。

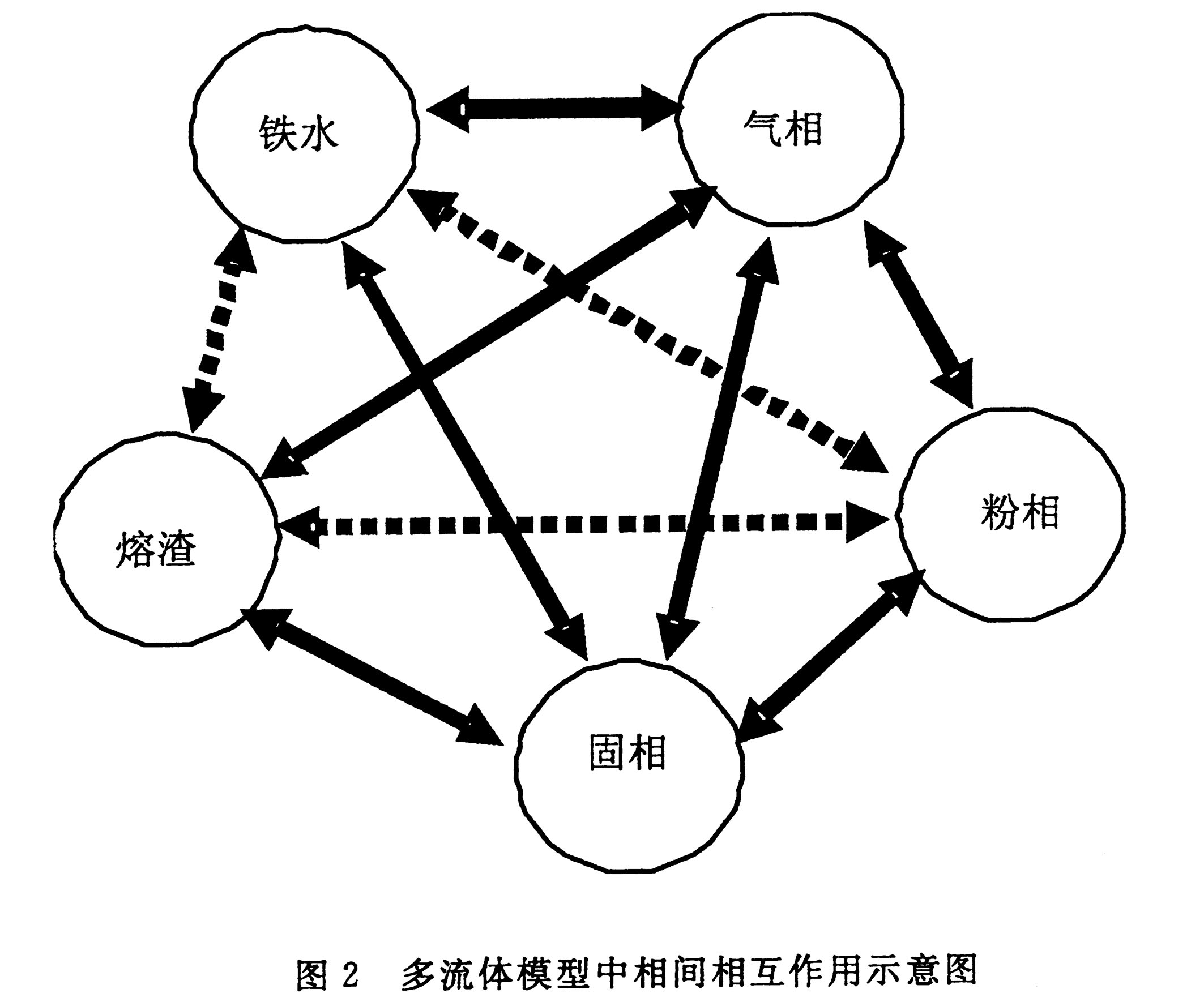
多流体模型中各相之间的相互作用如图2所示。图中实线代表动量、质量和能量的完全相互作用，点线代表质量的传输。模型认为气固两相与其他相之间均有完全的质量、动量和能量交换，而不连续相(液相和粉相)之间不进行动量交换，但通过化学反应和相变进行质量和能量交换。

多流体模型采用一系列偏微分方程对炉内各相的行为以及高炉冶炼过程进行高精度的数学模拟。由于各相之间同时且双向相互作用，故这些偏微分方程是强烈耦合的，须同时求解。所有方程可以用一个统一化的形式来加以描述。

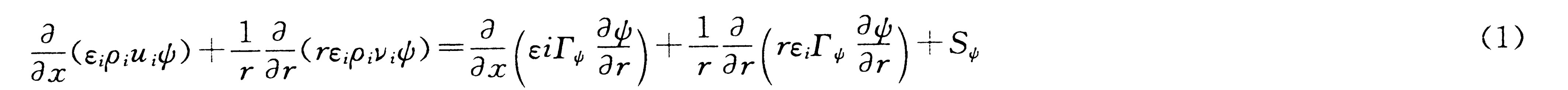
在方程(1)中，下标代表要考虑的各相，即气相、固相、铁水、熔渣和粉相。变量ψ代表求解的变量。通过改变ψ，分别代表质量、动量、能量方程以及连续性方程。ε_i代表相的体积分数。Г_ψ代表有效扩散系数，根据所求解的独立变量具有不同的意义。如对于动量方程，Г_ψ表示动力粘度；而对于能量方程，Г_ψ为导热系数。S_ψ为源相，主要是由于化学反应、相间相互作用、外力以及相变等因素而产生。

2．2 源相

由于化学反应和相变，质量方程具有质量源。模型中主要考虑了如下反应：铁氧化物间接还原；熔渣中FeO直接还原；回旋区的燃烧反应；焦炭气化溶损反应；水煤气反应和水煤气转变反应；Si迁移反应；渗C反应；熔化及相变反应；水分蒸发或者凝结反应等。并利用已有的实验研究成果对上述反应的速度进行了动力学公式化描述^［⁴^—7^］。

不同相间产生动量交换，主要是因为速度差的存在。模型中相间动量传输量通过下式计算。

能量方程的源相包括反应热和相间对流换热。模型通过下式计算相间对流换热量。

2．3 模型求解

模型计算时同时求解所有的方程。首先，在计算区域内利用BFC法^[11]进行网格化，如图3所示。相对于传统的直角正交坐标体系，BFC网格很好地解决了边界值设定问题，减少了边界溢出，从而加快了计算进度，提高计算精度。随后，利用控制单元体法^［¹²^］离散化所有方程。最后，采用SIMPLE法^[12]和迭代矩阵法求解所有离散的方程。

模型对边界条件进行如下设定^[4^—7]：1)没有物质穿过炉墙边界。对于和炉墙平行的速度，在应用滑动条件的同时还考虑了摩擦力对固体料速度的影响。炉墙外表面的温度参照实际值

设定；2)在风口处，速度、组成、温度和气粉相体积分数基于实际操作条件而具体设定。对固相和液相，风口处设定等同于炉墙处；3)在中心轴处，除了径向速度外所有变量的梯度为0；4)只有液相可以流过渣面，而对于其它相，渣面视为炉墙。渣面温度为渣面处铁水和熔渣温度的平均值；5)在料面处，固体炉料的成分和温度基于操作条件而具体设定，而其它变量不存在梯度变化。

整个求解过程分成三个部分，包括：首先是输人原始数据(如操作参数、炉型构造数据、模型常数初始值等)并生成网格；接下来是高炉模型计算的核心部分，循环迭代计算因变量、炉内各相物性和相间相互作用；最后输出结果并将结果保存用于后期数据处理。根据计算结果可给出炉内工艺变量(温度、压力、速度、反应速度、体积分量以及相物质组成等)的多维分布和生产指标(产量、利用系数、渣量、焦比、煤比、还原剂消耗总量以及炉顶煤气利用率等)的变化。

该模型的程序编写语言为FORTRAN 77，编译环境为Visual．FORTRAN 5．0。计算结果用Tecplot软件进行可视化处理，得到变量的多维分布图。

2．4 模型验证

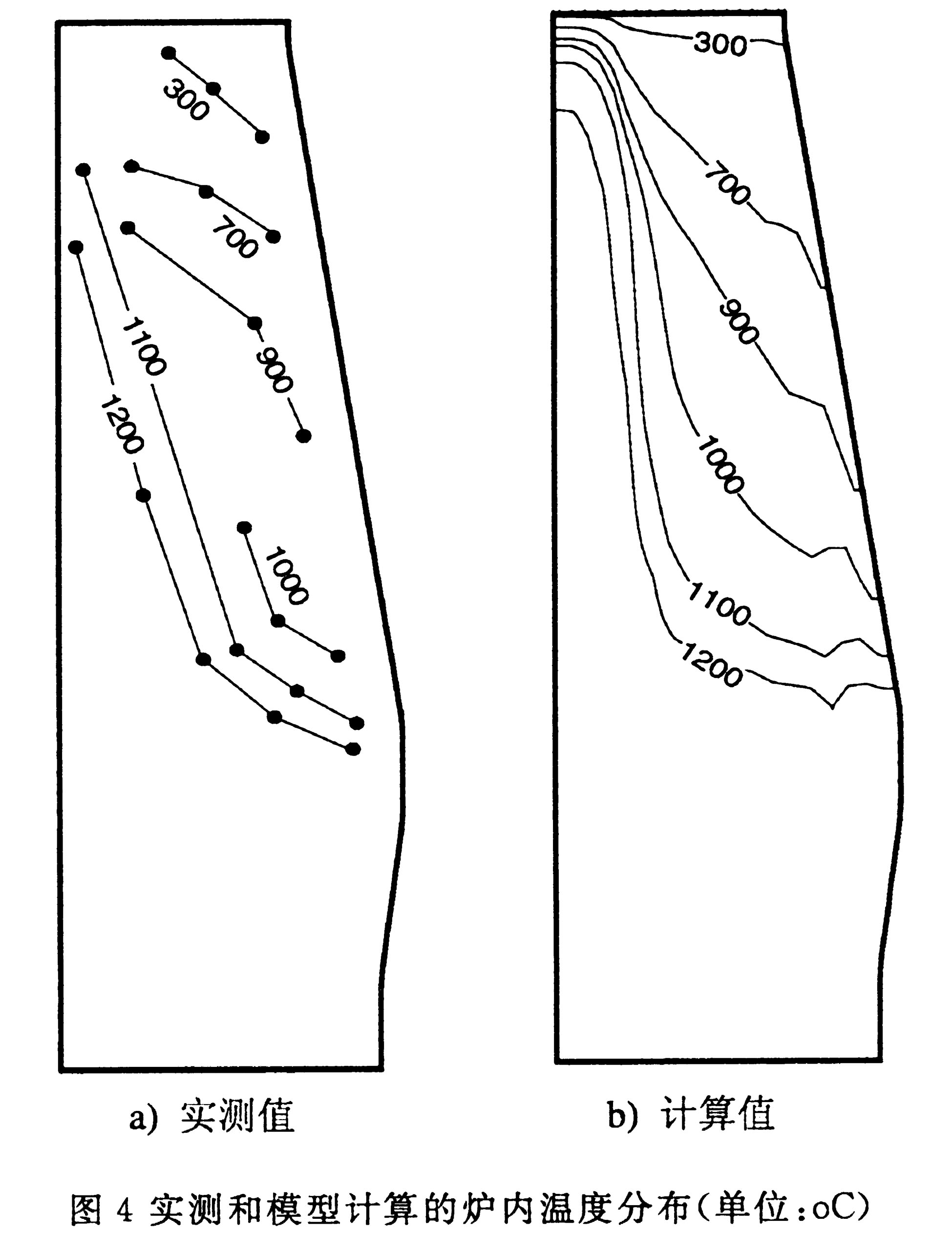
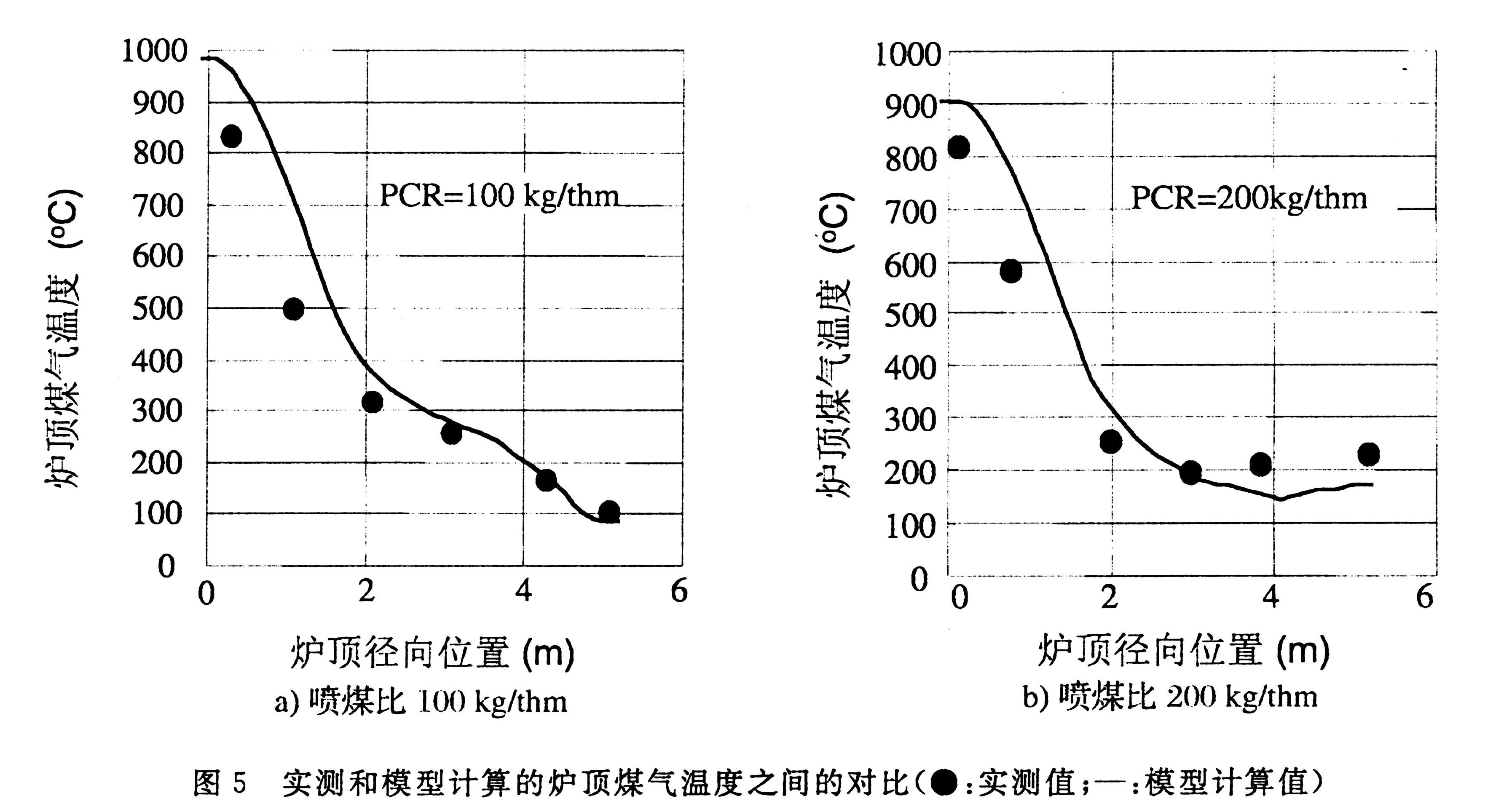
利用某实际运行高炉的生产数据对多流体数学模型的有效性和计算的精确度进行了充分验证。表4给出了模型预测值和实际高炉操作参数之间的对比，主要项的预测误差低于5％。图4给出了模型预测的炉内二维温度分布与实际测量值(由于炉内测温元件的限制，1200℃以上温度区域未能给出)。可以看出，模型基本预测了炉内温度分布走向，模拟值与测量值显示了良好的一致性。图5给出了模型计算和实际测量的炉顶煤气温度值对比。除了靠近中心轴线区域之外，在其他处模型计算值与实际测量值基本吻合。应该说，多流体模型合理地描述了炉内现象和准确预测了操作指标。

3 高炉数学模型的展望

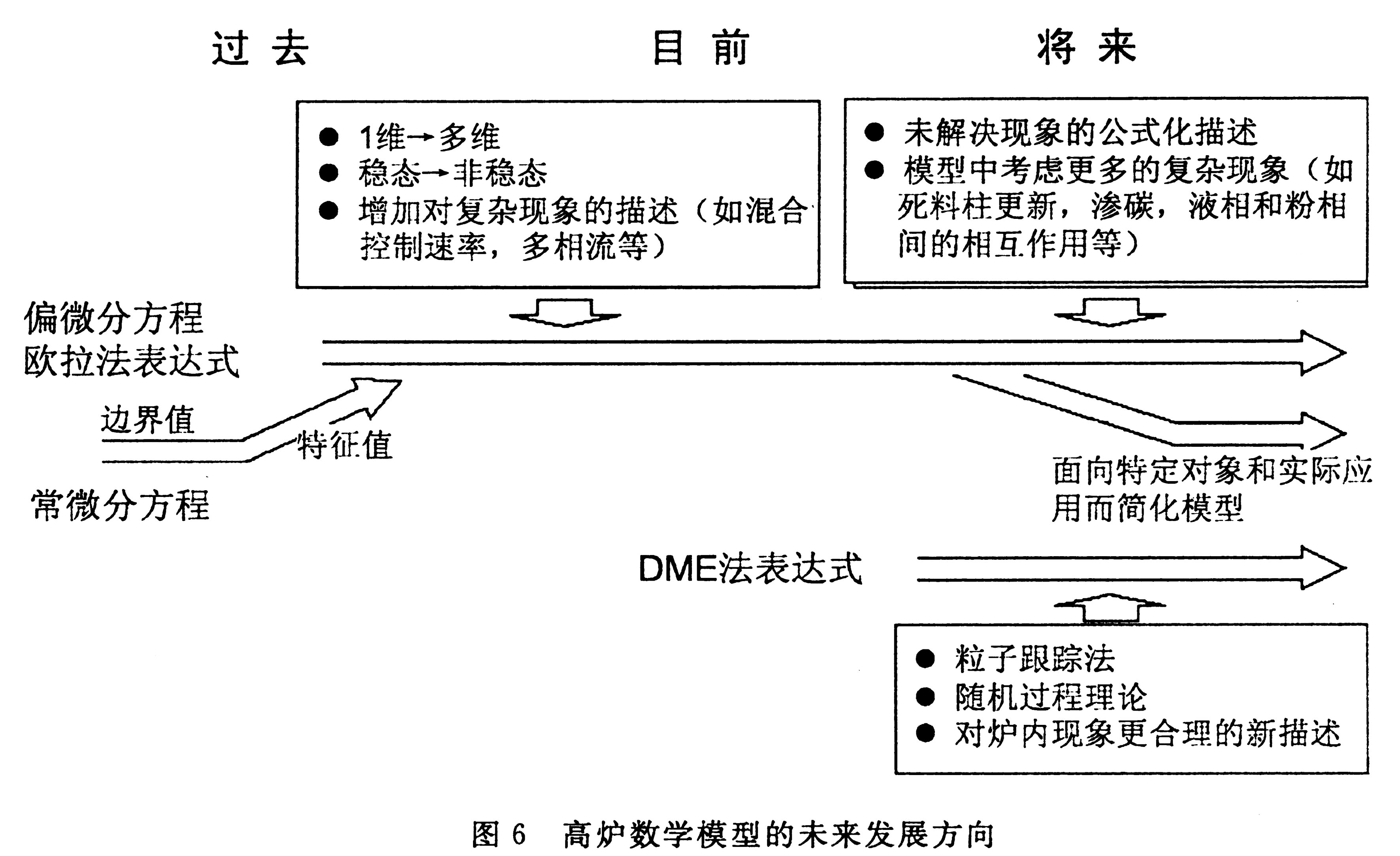
图6指出了高炉数学模型未来的发展方向，核心是提高数学模型的实用性和精确度。

首先是扩展和丰富目前的建模体系、思想和方法。为此，一些尚未解决的现象应在新的模型中加以考虑，包括：1)粉相和液相静态滞留和动态滞留的区分，以及两种滞留之间物质传输机制和速率；2)炉内固体物料粉化而导致的粉相产生机制及速率；3)脉石混合物在炉内的熔融现象和速率；4)铁水中微量元素的扩散机制和基于速度论的描述；5)液相和粉相之间的相互双向作用机制；6)生铁渗碳的机理和速率；7)死料柱更新的机理和速率。