结晶器振动参数对液态摩擦力的影响规律

结晶器振动参数对液态摩擦力的影响规律

周景一^1,2  刘文慧³  王博^1,2  刘震^1,2

（1. 华北理工大学冶金与能源学院，河北 唐山 063210,2. 河北省高品质钢连铸工程技术研究中心，河北 唐山 063000；3. 华北理工大学经济学院，河北 唐山 063210）

摘  要：连铸过程中，保护渣液态摩擦力对铸坯与结晶器之间的润滑起着至关重要的作用，通过建立结晶器同步振动模型，改变波形偏斜率、振动频率，将液态摩擦力控制在合理范围内，从而改善铸坯表面质量，减少拉漏情况。结果表明，波形偏斜率、拉速、振动频率和振程的增加对于结晶器上升过程中铸坯受到的拉应力均增大，而在下降过程中波形偏斜率与拉速的增加会导致坯壳受到的压应力是减小的，其余两个参数下的压应力是增加的。

关键词：同步振动模型；非正弦振动；液态摩擦力

Study on trial production of nitrogen micro-alloyed

reinforced bar

ZHOU Jing-yi1, LIU Wen-hui2，WANG Bo1，LIU Zhen1

(1. North China University of Science and Technology, College of Metallurgy and Energy , Tangshan 063000, China;2. Hebei Province High Quality Steel Continuous Casting Engineering Technology Research Center , Tangshan 063210, China; 3. North China University of Science and Technology, College of Economics, Tangshan 063210, China)

Abstract: In the continuous casting process, the liquid friction of the slag plays a vital role in the lubrication between the slab and the mold. By establishing crystallizer synchronous vibration model, the waveform deviation rate and vibration frequency are changed, and the liquid friction is controlled. Within a reasonable range, thereby improving the surface quality of the slab and reducing the leakage. The results show that the increase of the waveform deviation rate , the speed, the vibration frequency and the vibration increase the tensile stress of the slab during the ascent of the mold, while the slope of the waveform and the speed during the falling process. The increase will cause the compressive stress on the shell to be reduced, and the compressive stress under the other two parameters is increased.

Key words: crystallizer synchronous vibration model; non-sinusoidal vibration; liquid friction

结晶器振动与保护渣润滑是促进连铸快速发展的基础技术，为稳定、连续、高效地生产优质铸坯提供了技术支持。液态摩擦力对结晶器与铸坯之间的润滑起着至关重要的作用，结晶器振动与液态保护渣两者之间应当满足一定的关系，否则，连铸过程中易导致事故或铸坯缺陷。因此，研究振动参数对液态摩擦力的影响就显得十分重要。

本文基于某钢厂小方坯连铸结晶器非正弦振动波形，建立非正弦振动控制模型，分析振频、波形偏斜率α等对液态摩擦力的影响，阐述结晶器非正弦振动参数对液态摩擦力的影响规律。

1模型建立

1.1非正弦振动简介

非正弦振动不仅引入了正弦振动的因素[2]，还突破了正弦振动的限制，使结晶器振动具有最佳模式，能够有效减少铸坯与结晶器间的摩擦力，从而减轻铸坯振痕，提高铸坯质量。并且增加了独立振动参量——波形偏斜率α，增大了波形曲线调节能力，该参数有利于铸坯的脱模和润滑，从而弥补了正弦振动的频率、振幅不能同时满足脱模和润滑的不足。

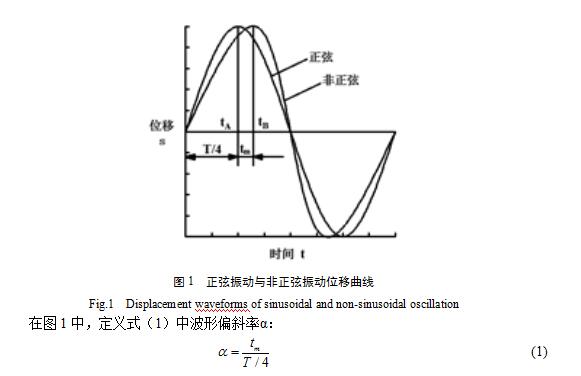
式中，tm为非正弦振动最大位移相对于正弦振动最大位移在时间上的滞后，s；T为振动周期，s。

非正弦振动主要特点[3-5]有：

（1）一个振动周期里，非正弦振动相比于正弦振动在相同的振幅和频率下，非正弦向下运动平均速度快、加速度大、时间短。

（2）在正滑动时间里结晶器振动速度v与拉坯速度vc之差减小。因此，作用在弯月面下坯壳的拉应力减小；

（3）在负滑动时间里v与vc之差较大，因此作用于坯壳上的压应力增大，有助于铸坯脱模；

（4）负滑动时间短，铸坯表面振痕浅。

1.2 同步振动模型建立

构建适合此钢种vc－f、h结晶器振动同步控制模型[6]。通过VB编程进行数学模拟，利用该模型模拟结晶器振动参数中的波形偏斜率α和振动频率对保护渣消耗量的影响。

vc—f、h同步控制模型的一般表达式为式（2）：

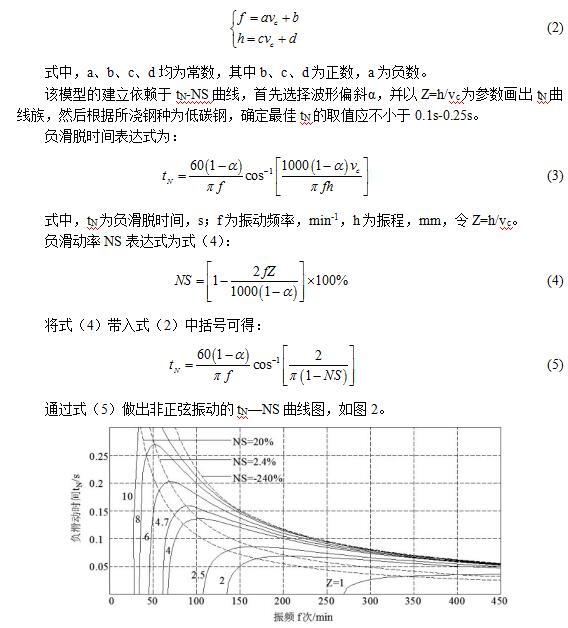
图2 非正弦振动的tN-NS曲线图[4]

Fig.2  The tN-NS curves of non-sinusoidal vibration

在图2中，过tN=0.1s点作一条水平线，分别与设计拉速范围内Z=4.7时的交点，对应的负滑动时间曲线上的两点，其横坐标分别对应在固定拉速下同步控制模型的临界频率和最高频率，然后由Z=h/vc及同步控制模型的拉速数值计算振程h。依据各参数间对应关系将所得数据代入式(2)，解方程组，即可建立需要同步控制模型。

基于上述对同步控制模型特点的分析，运用各参数间的对应关系，可进一步建立合理的vc—f、h同步控制模型。通过图2与各参数间的对应关系得出，可进一步建立合理的vc—f、h同步控制模型。对模型所做的基本假设为：不改变拉速，振幅，只改变结晶器振动参数中的波形偏斜率α以及振动频率，并且假设保护渣黏度及钢种类型，尺寸，非正弦同步控制。因此通过式(2)—(5)计算：推导出非正弦振动模型如式(6)，

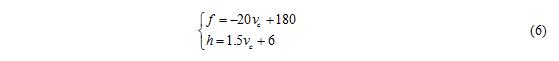
vc－f、h同步控制模型的特点是[7]：振程h随拉速vc的增加而增加，频率f随vc的增加而降低，同时tN近似恒定。tp随vc增加而增加。

2 不同振动参数下液态摩擦力比较

通过同步振动模型以及摩擦力计算公式，改变振动频率以及波形偏斜率α，分析两个参数对液态摩擦力的影响，获得两个参数较为合适的数值，保证铸坯表面质量，减少铸坯缺陷，增加金属收得率。

2.1 工艺条件

对非正弦反向振动，在拉速，保护渣确定情况下液态摩擦力与振动参数有关。下表为国内某钢厂的主要振动参数：

表1计算所用主要工艺参数

Table 1 Main technical parameters for calculating in the lubrication model

2.2 液态摩擦力的理论分析及计算方法

由牛顿黏性定律可知，铸坯和结晶器间的摩擦受到渣膜中液渣层的流动及分布的很大影响[8,9]。因此，液渣的流入速度对于计算结晶器和铸坯间的液态摩擦力有直接的作用。从而对结晶器润滑有影响，使铸坯质量受到影响。

保护渣在结晶器弯月面处的行为，在初期阶段对钢液的凝固和铸坯表面质量有很大的影响。所以对弯月面处的保护渣流入机制的研究是十分必要的。

结晶器与铸坯之间有两种渣膜形式：一种为固态渣膜，另一种是液态渣膜，其分布如图3所示，故想要计算结晶器与铸坯之间的摩擦力，就必须分别计算固态和液态渣膜的摩擦力。

铸坯与结晶器间的总摩擦力等于铸坯与结晶器间固态和液态摩擦力之和为式（7）：

式中：

Fl—单位面积液体摩擦力，Pa；

η—保护渣的黏度，Pa·s；

vm—结晶器运动速度，m/min；

vc—拉速，m/min；

dl—液渣层厚度，mm。

由上式可以得出，铸坯与结晶器之间液体摩擦力Fl主要是由液体渣层的厚度、保护渣的黏度及结晶器振动速度和拉坯速度决定。

结晶器向上振动速度公式为式（9）：

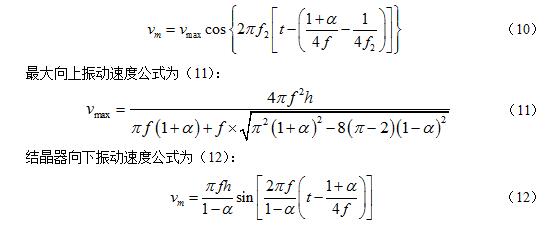
通过某钢厂提供的数据可知液渣层厚度为6~10mm，通过式（11）、（12）即可求出结晶器非正弦运动时上升和下降时结晶器的运动速度，再将结果代入式（8）可以求得液态摩擦力。

2.3 波形偏斜率α对液态摩擦力的影响规律

由式可以看出，波形偏斜率α对于结晶器振动起着重要的作用，因此，在确定vc=1.5m/min、f=160次/min、h=5.45mm下，改变波形偏斜率α，采用表中的工艺参数。通过式（8）、（11）和（12）计算得出，波形偏斜率α对结晶器上升和下降时的速度及受到的液态摩擦力的影响。

图3所示当改变波形偏斜率α的情况下，波形偏斜率α与保护渣消耗量的关系图。

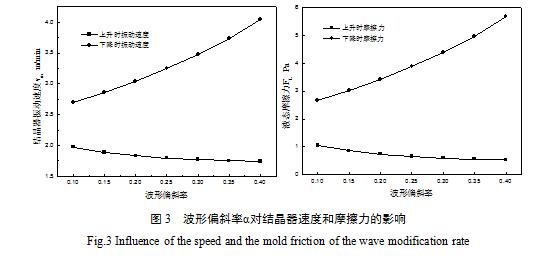
通过图3中可以看出，当振动时间为t=0时，为上升速度最大，随着波形偏斜率α的提高，在上升时，结晶器振动速度和液态摩擦力呈现下降趋势；当振动时间t=T/2时，下降速度最大时，呈现为上升趋势。这是因为在式（11）、（12）中波形偏斜率α对上升速度和下降速度的影响是相反的。当拉速不变时，也就导致其对上升及下降液态摩擦力的影响是相反的。

2.4 振动频率对液态摩擦力的影响规律

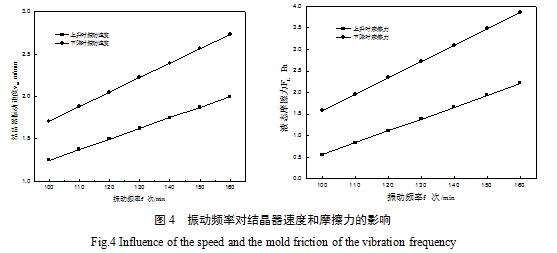
在α=0.1、vc=1.5/min、h=5.45mm条件下，改变振动频率f，在频率f=100~160次/min的情况下计算对结晶器上升和下降时的速度及受到的液态摩擦力的影响。

图4所示为改变振动频率f的情况下，振动频率与振动速度、摩擦力之间关系图。

通过图4中可以看出，随振动频率f的增加，当振动时间t=T/2时，下降速度最大。此时，在结晶器上升与下降时，结晶器振动速度和液态摩擦力均表现为增加趋势。这是因为在式（11）、（12）中振动频率f是上升速度和下降速度的增函数。当拉速不变时，也就导致其对上升及下降液态摩擦力的影响趋势是相同的。

2.5 拉速对液态摩擦力的影响规律

在α=0.1、f=160次/min、h=4.9mm下，改变拉速vc=1.0~2.0m/min的情况下，通过式（11）、（12）可知发现拉速vc与结晶期振动速度的快慢无关，因此只能观察拉速vc的改变对液态摩擦力的影响。采用表中的工艺参数。

图5所示当改变拉速vc的情况下，结晶器上升及下降时受到的液态摩擦力的关系图。

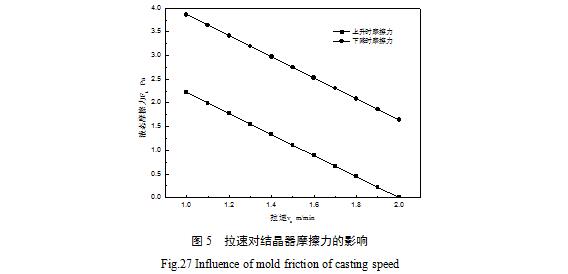
通过图5和式（8）中可以得出，当增加拉速vc时，结晶器振动时，受到的液态摩擦力逐渐减少。同时，当波形偏斜率α、振动频率f、振程h一定时，可以得出结晶器上升及下降速度是一定的，因此液态摩擦力的大小只与拉速有关。

2.6 振程对液态摩擦力的影响规律

在α=0.1、vc=1.0m/min、f=160次/min，在改变振动冲程h=4.9~6.0m的情况下结晶器上升和下降时的速度及受到的液态摩擦力的影响。采用表中的工艺参数。

图6所示当改变振动冲程h的情况下，振动冲程h与结晶器振动速度及摩擦力之间的关系图。

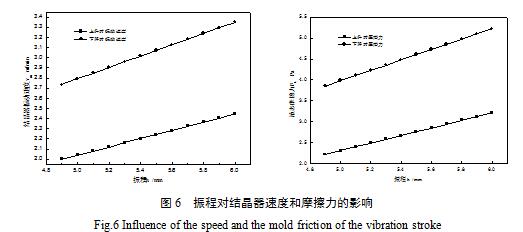
其它条件不变，随振程h增加，此时的上升与下降速度都是增大的，上升速度由1.998增大到2.447m/min，下降速度由2.734增加到3.351m/min，导致摩擦力增大，上升时摩擦力增大3.22Pa，下降时摩擦力增加到5.22Pa。

3 结论

1）当只改变波形偏斜率α，其他条件保持不变。随着波形偏斜率α增大，结晶器上升速度与上升时的液态摩擦力均呈减小趋势，而下降速度与下降时的液态摩擦力则成增加趋势，所以，较大的波形偏斜率α对结晶器运动时时的摩擦力和坯壳凝固有影响；

2）其它条件不变，只改变拉速vc。因为结晶器振动速度与拉速无关，所以，拉速对结晶器振动速度没有影响，但是拉速增大会使液态摩擦力减小，使坯壳受到的压应力减小；

3）当只改变振动频率f，其他条件保持不变。当振动频率增大时，结晶器振动速度在上升和下降时都是增大的，使得液态摩擦力都增大，对铸坯受到的压应力增大；

4）其它条件不变，随振程h增加，此时的上升与下降速度都是增大的，导致摩擦力增大，是坯壳受到的拉应力减小。

因此，通过以上分析得出，波形偏斜率α、拉速vc、振动频率f和振程h的增加对于结晶器上升过程中铸坯受到的拉应力均增大，而在下降过程中波形偏斜率α与拉速的增加会导致坯壳受到的压应力是减小的，其余两个参数下的压应力是增加的。

参考文献

[1] 文胜. 酒钢结晶器非正弦振动连铸工艺实践[J]. 山西冶金, 2014(2):61-63.

[2] 孟祥宁, 朱苗勇. 连铸结晶器非正弦振动波形构造及参数研究[J]. 中国机械工程, 2007, 18(15): 1779-1782.

[3] 李宪奎, 朱清香, 郑学然等. 结晶器非正弦振动波形及参数研究[J]. 钢铁, 1998, 33(11): 26-29.

[4] 马春武, 王虎祥, 李智等. 连铸结晶器非正弦振动波形的研究[J]. 铸造技术, 2013, 34(2): 214-218.

[5] 米源. 板坯连铸结晶器非正弦振动技术的应用[J].炼钢, 2006, 22(3): 6-9.

[6] 冯科, 韩志伟. 板坯结晶器液压振动同步控制模型的优化设计[J], 铸造技术, 2009, 30(10): 1326-1329.

[7] 李宪奎, 于敏之, 赵红雁. 结晶器反向振动同步控制模型[J]. 重型机械, 2001, 2: 16-19.

[8] 訾福宁. 板坯连铸结晶器电动缸非正弦振动技术与应用[J]. 连铸, 2013(1):22-26.

[9] NAKAMORI YUKIO. FUJIKAKE YOUICHI. Development of measuring system for friction in continuous casting mold[J]. ISIJ Intemational, 1984(4):1262-1268.